You’ll never take my (Degrees of ) FREEEEDOM

I’ve had a lot of questions regarding the correct number of Degrees of Freedom for a t-test, and so I thought it was worth doing a quick post on the subject. One of the reasons for all these questions is, I suspect, the fact that I messed up. I got the degrees of freedom all confused for the examples I gave in my last post on the subject. The mistake I made was assuming that the degrees of freedom value for t-tests in a multiple regression were the same as for regular t-tests. Well I was wrong about that.

Now, as with everything else related to multiple regressions, getting a simple answer to this question is somewhat harder than you would think. I have looked at more websites on multiple regressions than any sane person should and I am still not 100% sure I have the answer. As such the information below will represent what seems to be the consensus opinion of the various sources I looked at. As always I would recommend you talk to your supervisor and go with what every they say rather than take my word as gospel, but this should at least put you on the right path.

Firstly, some basic degrees of freedom information in relation to t-tests. If you are just running t-tests on their own then degrees of freedom are fairly straight forward. If you are carrying out a one sample t-test, where you are looking to see if the average value of your sample differs significantly from the population mean, your degrees of freedom value is the number of people in your sample (N) minus 1. However, if you are carrying out a two sample t-test, where you are looking to see if the mean of two populations is significantly different based on your sample means, the degrees of freedom are the number of people in sample one (N₁) plus the number of people in sample two (N₂) minus 2. So to clarify:

One sample t-test:

DF = N – 1

Two sample t-test:

DF = (N₁ + N₂) – 2

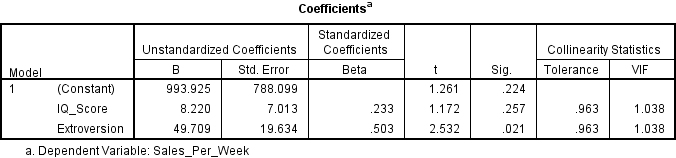
Right, so that’s the simple stuff out of the way. Let’s delve into the weird and confusing world of multiple regressions once more (it’s not actually that confusing, don’t worry). Now in multiple regressions t-tests are used when looking to see which of the predictor variables contributed to our results. To find this out we turn to the Coefficients table. Here’s one I prepared earlier:

This table represents to simplest multiple regression you can have, in that it only has two predictors, IQ scores and extroversion scores. When describing your results you need to mention the Beta value, as well as the t-test and significance values. But what about those pesky degrees of freedom? Now depending on which source you look at, a couple of mine can be found here and here, the degrees of freedom for the t-test may be reported as either N-K or N-K-1. Well that’s confusing…only not really. It simply depends on how they are defining K.

So what the hell is K? K represents the number of predictors that you have in your experiment. So above we have a K value of 2, because, obviously, we only have two predictors. Now if you are viewing it this way then your degrees of freedom represent the number of people in your study (N) minus the number of predictors (K) minus 1. So what about those people who claim it is N-K, are they wrong? Well no, and that’s because they are including the constant as one of the predictors. So looking at the table above you see we have two predictors and a constant, that’s three things (and later I will teach my grandmother to suck eggs). Now obviously subtracting a K value of 3 is the same as subtracting a K value of 2 minus 1, so which ever way you want to look at it is good with me. So let’s finish this off shall we.

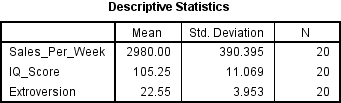
Taking the data from the two tables above we can, finally, report the correct results.

The analysis shows that intelligence level did not significantly predict value of sales per week (Beta = .23, t(17) = 1.17, ns), however extroversion level did significantly predict value of sales per week (Beta = .50, t(17) = 2.53, p < .05).

So there you go. Sorry if my mistake caused you any confusion. I want to finish by thanking one of my commenters, Grayden, for pointing out my error and telling me what the answer should have been. Hopefully my posts on multiple regressions are now correct.